Nepnep2025 Lattice Bros

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#已知α的极小多项式为三次多项式f(x),即f(α)=0,且α≈54236.606188881754809671280151541781895183337725393

#上述极小多项式的常数项为a0

from secret import a0,alpha

import gmpy2

from Crypto.Util.number import long_to_bytes

import random

from math import sqrt,log2

d=981020902672546902438782010902608140583199504862558032616415

p = d - a0

k=sqrt(log2(p))+log2(log2(p))

B = 2**30

assert B < p/2**k

m = 30

assert m > 2*sqrt(log2(p))

samples = []

betas = []

f = open("samples.txt",'w')

for _ in range(m):

  t = random.randint(1, p-1)

  beta = random.randint(-B + 1, B - 1)

  a = (t * alpha - beta) % p

  samples.append((t, a))

  betas.append(beta)

f.write(str(samples))

for i in range(0,30):

  assert (betas[i]-samples[i][0]*alpha+samples[i][1])%p == 0

#flag = long_to_bytes(alpha)

首先我们需要恢复的是a0的值

我们可以利用LLL算法来恢复一定次数的极小多项式，对于多项式来说我们有 a0 + a1x + a2x2 + a3x3 = 0

$$ \begin{pmatrix} a_0&a_1&a_2&a_3 \end{pmatrix}\begin{pmatrix} 1 &0& 0 & a^0M\\ 0& 1 & 0 & a^1M\\ 0&0& 1 & a^2M\\ 0&0& 0&a^3M \end{pmatrix} $$

这里我们M我们根据a的的精度选择10^50来配平

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
a=54236.606188881754809671280151541781895183337725393

M=10**50

Matrix=matrix(ZZ,[[1,0,0,a^0*M],

         [0,1,0,a^1*M],

         [0,0,1,a^2*M],

         [0,0,0,a^3*M]])

L=Matrix.LLL()

a0=L[0][0]

print(a0)


这里其它师傅那里看到了sagemath的内置函数可以求解

1
2
3
4
5
6
7
8
9
10
11
alpha = 54236.606188881754809671280151541781895183337725393

 

f = algdep(alpha, 3)

a0 = f(0)

print(f)

print(a0)

得到a0之后我们可以直接求出p

之后就是HNP问题了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from Crypto.Util.number import *

a0=-159534088683654

lis = [(541847931463604073209188621415697353813245102261880389530448, 293760933113243563398917466885108625646262447370201484418246), (235213326900086489464935804156966465366154623411555613791270, 660823982268225103178763707015491421784294988488272636270997), (826464884761457937459245903152143755707241416981488127320435, 428521663319038461250005113612781686761766888058391496085911), (589542000504317435156560078533519448295689695687499354390208, 155284353896000150766154807679279597476176668344402166959399), (968823371588600973965757332601758200815345862153455338808286, 870008943690791009196027169525956126827736285614393106689402), (621636099728440147413990266662022925118216803638588918660041, 265635912066749696542909843111997941904342442664219734956888), (426696569424050102229606043215592727790577655338668728275370, 279313121876980354011480010042682666651614765507190502627689), (89450479064580125731654556963306718472532905610952012502649, 465933125964565419295325650759566635253450915499965633327941), (480355476500393865742379469913983270769356894135485925662119, 894041172171871806404285309781862268351135623868845025443422), (842436524669577199024236805258573090764419350786291073287889, 345478552143958037534551648319293899442551000874041707820740), (650054674429185550652935714084022116516082323269321462104664, 441999979283903658157822753439653947343822546158589507765994), (46289431385578693366971976442426853079852982529357847290686, 625618376463384339878849844467050454204685252824782609369180), (71444185449163133531919043374545893927347050624346741281881, 955925578289311966288639224625142299309823207245807788495453), (192579726169321656812883068526498248523814846320328766176253, 626481822474054336470183912297952839011392733501646931370367), (736527635648804640774976580747540045854351230084566721853611, 276626211757586963928788091386096607703513204646314683038338), (177922521867185878959621840269164617147915792720210315529733, 541058782621716573816245900423919799500476442285991532228641), (40610451174818168154306630612571678739921107216052349044576, 727642592899858828601137105077611015328512898368636299587376), (385012983728389322601149562441674995471397288632464238356283, 353921151307105661267278594470212933060655245893209524497156), (750447975601038834764379841158092390933760641866111445401426, 391626416964965737035878375834907580903143512300198923948189), (115058604943298010958881205548782439407592353731185670266593, 491630592857258949793489206081490523001249620510479961058022), (327389234395954477946639629629085910688793716425320663599360, 24975272330009592102362429346350824580378490147041708568130), (115595274689129534885608766476695918464309130165432995990883, 757961876891952019297626599379744405302595090402128271144165), (950804723308776351161744501221236453742418549093165078282534, 20307246759635231945223392614290397512873344480184942904518), (724537610412063699714461780160573528810830178440136810747811, 149681928388378582933943374524511804362928290938917573644613), (340891278018589324130004945217960336392205386747747011263373, 683307718413135477104477081812052183267507312278283317237187), (104379682905784169840335131193505192063050242530811180817410, 715010230598797717533306270232399781090458356371977748416491), (644160326926600986730919713173510327120201404569141824224075, 127877985489410167008195578625004740882394608402141169695352), (549253388716005399852261816416312267100135940382820676807345, 210560134643237517255193955173709174155305784935427470113433), (968265711632086435506163736279856957220961064226797549228006, 273174723915971720522674140326199419265943707917542063022561), (704367622558261900937184683100177434487519780290678439135652, 959106497548134540301589019840013331842784496835379005298630)]

d=981020902672546902438782010902608140583199504862558032616415

p = d - a0

if p.is_prime():

  B = 2**30

  ge = [[0] * 32 for _ in range(32)]

  for i in range(30):

    ge[i][i] = p

    ge[-2][i] = lis[i][0]

    ge[-1][i] = lis[i][1]

  ge[-2][-2] = B/p

  ge[-1][-1] = B

 

  Ge = Matrix(QQ, ge)

  L = Ge.LLL()

  

  for row in L:

    if abs(row[-1]) == B:

      

      print(long_to_bytes(p-int(row[-2]*p/B)))

Nepnep2025 ezRSA2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
from Crypto.Util.number import getStrongPrime, getRandomNBitInteger, GCD, inverse, long_to_bytes, bytes_to_long, sieve_base

from flag import flag

def gen_parameters(gamma=0.33, beta=0.33):

  p = getStrongPrime(1024)

  q = getStrongPrime(1024)

  N = p*q

  phi = (p-1)*(q-1)

  while True:

    d = getRandomNBitInteger(int(2048*beta))

    if GCD(d, phi) == 1:

      break

  e = inverse(d, phi)

  

  hints = []

  M = 1

  for i in range(1, len(sieve_base)):

    li = sieve_base[i]

    hints.append(d%li)

    M *= li

    if M.bit_length() >= 1024*gamma:

      break

  

  return e, N, hints

def main():

  e,N,hints = gen_parameters()

  print(f'e={hex(e)}')

  print(f'N={hex(N)}\n')

  print(f'hints={hints}\n')

  

  flag_prefix = b'NepCTF{'

  assert flag.startswith(flag_prefix)

  assert flag.endswith(b'}')

  

  pt = bytes_to_long(flag[len(flag_prefix):-1])

  ct = pow(pt, e, N)

  print(f'ct={hex(ct)}')

  

main()

"""

e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29

N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

hints=[1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e

"""

审计代码发现这里是关键函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
hints = []

 M = 1

 for i in range(1, len(sieve_base)):

   li = sieve_base[i]
   
   hints.append(d%li)
   
   M *= li
   
   if M.bit_length() >= 1024*gamma:
   
     break

 


 return e, N, hints

这里我们可以得到hint的同余方程组 $$ \left\{ \begin{array}{l} \operatorname{hint}_{0} \equiv d \ (\bmod \ sieve_base[1]) \\ \operatorname{hint}_{1} \equiv d \ (\bmod \ sieve_base[2]) \\ \cdots \\ \operatorname{hint}_{r} \equiv d \ (\bmod \ sieve_base[i]) \end{array} \right. $$

同时还可以得到M的等式 $$ M=\prod_{i=1}^{len(sieve_base)}sieve_base[i] $$

我们可以先用crt来恢复部分的d

之所以这里只能恢复部分的d是因为

crt可以让我们从 d mod  li 的这些余数中，计算出 d mod  M

所以我们得到的是d在模M下的值，即 d ≡ d0 mod  M

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from Crypto.Util.number import *

 

e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29

N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

 

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e

 

hints = [1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

dd = CRT(hints, list(sieve_base)[1:len(hints)+1])

tmp = prod(list(sieve_base)[1:len(hints)+1])

print(dd)

这里求出了d0即是部分的d，部分私钥泄露会想到用Cooper来打

这里看到RSA的等式 e(d0 + k0 * M) − 1 = k1(N − p − q + 1) d=d0+k*M

有等式 e * (d0 + k * M) − 1 = k2(N − p − q + 1) 这里考虑用⼆元copper来打，先对等式进行变形 1 − e * d0 + k(N + 1 − r) ≡ 0 (mod  e * M) 这样的式子就可以打了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
from Crypto.Util.number import *

 

e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29

N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

 

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e

 

hints = [1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

d0 = CRT(hints, list(sieve_base)[1:len(hints)+1])

print(d0)

from Crypto.Util.number import *

import gmpy2

import itertools

def small_roots(f, bounds, m=1, d=None):

 if not d:

 d = f.degree()

 print(d)

 R = f.base_ring()

 N = R.cardinality()

 f /= f.coefficients().pop(0)

 f = f.change_ring(ZZ)

 G = Sequence([], f.parent())

 for i in range(m + 1):

 base = N ^ (m - i) * f ^ i

 for shifts in itertools.product(range(d), repeat=f.nvariables()):

  g = base * prod(map(power, f.variables(), shifts))

  G.append(g)

 B, monomials = G.coefficient_matrix()

 monomials = vector(monomials)

 factors = [monomial(*bounds) for monomial in monomials]

 for i, factor in enumerate(factors):

 B.rescale_col(i, factor)

 B = B.dense_matrix().LLL()

 B = B.change_ring(QQ)

 for i, factor in enumerate(factors):

 B.rescale_col(i, 1 / factor)

 H = Sequence([], f.parent().change_ring(QQ))

 for h in filter(None, B * monomials):

 H.append(h)

 I = H.ideal()

 if I.dimension() == -1:

  H.pop()

 elif I.dimension() == 0:

  roots = []

  for root in I.variety(ring=ZZ):

  root = tuple(R(root[var]) for var in f.variables())

  roots.append(root)

  return roots

 return []

e=0x73915608ed64c9cf1a2279684cab4f4a78fba229d45d4f860971a241481363470a19cb0dc0d00f816b5befdaca017cf71483e96ef17b36179012f5194a0e6bf481bb06c2644f74c6812efb65d05c00631f282d6aa55c0bc140a1830b95a1cf4b6024cb0db53f2c2189897c41f22e2eec773723f531ec4bfa537fae6de5fe480cf46fe17850f7eb47df08194d95db3d26ac923b26e110ee645239ab586bbc546ddc5906f280a106edbb727ccb05536b5a3f5c0ebcf865c95ce58be54f7f3547aa53baa218b0dfa98e42d925fa341e45f94a3b16b0c83802660c7f34de3336cb21f219073cf8e9f5e39d47f0a9a9ee7c255f09a6add9a2f7a47960f4a853183d29

N=0xba8956e81394f3f1265ca5d9c4ad1ab0078bb43c4b80a231ab2cc62246ae45f66a562252622aed2cbbfc08647ef2fec0f97a632bf2242845f4b3af0c427cec3d90f42e90278a5a0feeed0922a8cd2278074ac54e9cfc0e96ff68f8d8f266dd87dc1cc59c2895ec884de2022311767f6a9a7e0bd288c79620e28b83bb3c8d8ad1047c839d6ccf5544eaf434a5f00b951769ab3121298d04b63a162757beb3d49917cd0c9e02ee1ac29398c8130961d5a2f2833aba1e538edb7bb97071f40fae543d1622f0c9206c6d4d8abb2ac1b93ebfb603c2f3a909ede357ade4043550fe540d13a4e87db8d731fe130f15a43a1a00364f5da2d87f7b660c3a04e734218a11

hints=[1, 3, 0, 3, 9, 16, 10, 14, 5, 11, 21, 18, 30, 30, 38, 2, 20, 62, 66, 1, 22, 56, 41, 13, 78, 59, 51, 6, 57, 117, 73, 75, 96, 112, 50, 93, 158, 97, 146, 8, 65, 96, 186, 161, 90, 131, 46, 32, 140, 133, 50, 43, 151, 234]

ct=0x101b284ad196b5bbd3d3df00a7d3577caeb29c681bdd122582b705afc671febf45d4f3786640e55aadd6a31ecc49175f97b772720f1735f8555f768b137a4643cd6958f80a3dfca4d0270ad463d6dde93429940bd2abb5ad8408b0906fa8d776544a1c50cc0d95939bef4c3fb64d0b52dca81ff0f244fc265bfc0bc147435d05f8f1a146e963a1403b3c123b4d6e73d1fd897109995009be1673212607f0ea7ae33d23f3158448b05c28ea6636382eee9436c4a6c09023ead7182ecd55ac73a68d458d726e1abc208810468591e63f4b4c2c1f3ce27c4800b52f7421ccab432c03e88b3b255740d719e40e0226eabb7633d97ed210e32071e2ac36ed17ef442e

beta = 0.33

M = prod(list(sieve_base)[1:len(hints)+1])

PR = PolynomialRing(Zmod(e*M), 'x,y')

x,y = PR.gens()

f = x*(N+1)-x*y-(e*d0-1)

bounds =((e*2**int(2048*beta)) // N ,2**1024)

roots = small_roots(f, bounds)[0]

print(roots)

k=int(roots[0])

r=int(roots[1])

d = (k*(N+1-r) + 1) // e

m = pow(ct, d, N)

m = print(long_to_bytes(m))

DASCTF2025 Strange RSA

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
import random

from secret import flag, hint

from Crypto.Util.number import getPrime, GCD, bytes_to_long, inverse

def generate_flag_params(keysize=256):

  while True:

    p, q = getPrime(keysize), getPrime(keysize)

    N = p * q

    A = (p**4 - 1) * (q**4 - 1)

    while True:

      u = random.randint(2, 1 << 26)

      v = random.randint(2, 1 << 26)

      if GCD(u, v) == 1:

        break

    w = random.randint(-(v * N) + 1, v * N - 1)

    numerator = w + A * v

    if numerator % u != 0:

      continue

    e = numerator // u

    if e <= 0 or GCD(A, e) != 1:

      continue

    return {'N': N, 'u': u, 'v': v, 'e': e}

def generate_hint_params(u, v, keysize=512):

  p, q = getPrime(keysize), getPrime(keysize)

  N = p*q

  phi = (p-1)*(q-1)

  e1, e2 = 0, 0

  while True:

    try:

      x = getPrime(256)

      d1 = (v+u)*x

      d2 = (v-u)*x

      e1 = inverse(d1, phi)

      e2 = inverse(d2, phi)

      break

    except:

      continue

  return {'e1': e1, 'e2': e2, 'N': N}

def encrypt(flag, hint):

  params = generate_flag_params()

  N1, u, v, e1 = params['N'], params['u'], params['v'], params['e']

  e2, e3, N2 = generate_hint_params(u, v)

  flag_ct = pow(bytes_to_long(flag), e1, N1)

  hint_ct = pow(bytes_to_long(hint), random.choice([e2, e3]), N2)

  return {

    'flag_ct': flag_ct,

    'hint_ct': hint_ct,

    'N1': N1,

    'N2': N2,

    'e1': e1,

    'e2': e2,

    'e3': e3

  }

if __name__ == '__main__':

  res = encrypt(flag, hint)

  print(f'flag ciphertext: {res["flag_ct"]}')

  print(f'hint ciphertext: {res["hint_ct"]}')

  print(f'N1: {res["N1"]}')

  print(f'N2: {res["N2"]}')

  print(f'e1: {res["e1"]}')

  print(f'e2: {res["e2"]}')

  print(f'e3: {res["e3"]}')

  \# flag_ct = 3304275694820454674685997231149613707569155279977829020394149986905099581809908257209756187158847732534210083918959247704733651870464045546533643246315075

  \# hint_ct = 92640601724170927054025127187177279602224180611842629533022715235486983387366622510122048491911345879387849666443268190910926361909061627381467094692466413099146606063231426714299807657192175870860604519763163994726401817194260892563952333383283965304691493157326860489170198604706615586060763745868090002740

  \# N1 = 7348121907179526913580177851026954330752768738291896096735058973559480119932817354982584848148959373549116865913413457772773261195054845650206020666330991

  \# N2 = 107505436651153972868256172927458682863384962980950626300023016225072477035531962210081972740487894427658040878262205693734911880215972363343499849037411996091935215324499998500280001539069563664673471788918797180228775246203241297837846844704493266809513512780251834022988415242950525647295962207347676276159

  \# e1 = 46483493180168456907876964472003342599505589423824575610973682748466876137876722746536417805454147792987530564436875226141952843276430892859209813871491418332469407742523023206446900477888407552315053106617523965303933309326359897043169707586465120984991379773865649114063608940450932600749494216244527815359

  \# e2 = 45077696779822473738225957332830108221557084179697632022751654753481408195463722246182963143687869636871041685807164964262563391336227375090607312507452525793175139773473714173537596307343530651384764927086658506652872283207536853955899859738928440798959619962363749291669111681250920552149008464286936309009

  \# e3 = 23550626043318531686392597908767473613369638520090152127370654817423383818034484441592543825793324637247596257173381762273905254049903422039592935871962187682259917270517329309332496277455914971819636329971254701142348560600765095893262007065327568577225527780321485212099754825195447682395092115782178271206767089362177657624379873520519398661669609981034432208973165597218334711366939977911593062941916527006025062935544853270685363226130039339985009309168493915830639441795502226746782561939904234398557509011544985054339634943750567054335128439233603858646704023191283512166289385748291358620388592170413196949907

题目分为两个部分,一部分是对hint的加密，一部分是对flag的加密

我们先解出hint

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def generate_hint_params(u, v, keysize=512):

  p, q = getPrime(keysize), getPrime(keysize)

  N = p*q

  phi = (p-1)*(q-1)

  e1, e2 = 0, 0

  while True:

​    try:

​      x = getPrime(256)

​      d1 = (v+u)*x

​      d2 = (v-u)*x

​      e1 = inverse(d1, phi)

​      e2 = inverse(d2, phi)

​      break

​    except:

​      continue

  return {'e1': e1, 'e2': e2, 'N': N}

这里我们发现可以用Boneh-Durfee攻击来求d1，d2

这里先看u,v和d1，d2的生成表达式

1
2
3
4
5
6
7
8
9
u = random.randint(2, 1 << 26)

v = random.randint(2, 1 << 26)

x = getPrime(256)

d1 = (v+u)*x

d2 = (v-u)*x

从这里我们知道d1,d2<2256 + 26,这里d > N292

满足Boneh-Durfee攻击，这里格的大小取8

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
348
349
350
351
352
353
354
355
356
357
358
359
360
361
362
363
364
365
366
367
368
369
370
371
372
373
374
375
376
377
378
379
380
381
382
383
384
385
386
387
388
389
390
391
392
393
394
395
396
397
398
399
400
401
402
403
404
405
406
407
408
409
410
411
412
413
414
415
416
417
418
419
420
421
422
423
424
425
426
427
428
429
from __future__ import print_function
import time

############################################

# Config

##########################################

"""
Setting debug to true will display more informations
about the lattice, the bounds, the vectors...
"""
debug = True

"""
Setting strict to true will stop the algorithm (and
return (-1, -1)) if we don't have a correct
upperbound on the determinant. Note that this
doesn't necesseraly mean that no solutions
will be found since the theoretical upperbound is
usualy far away from actual results. That is why
you should probably use `strict = False`
"""
strict = False

"""
This is experimental, but has provided remarkable results
so far. It tries to reduce the lattice as much as it can
while keeping its efficiency. I see no reason not to use
this option, but if things don't work, you should try
disabling it
"""
helpful_only = True
dimension_min = 7 # stop removing if lattice reaches that dimension

############################################

# Functions

##########################################

# display stats on helpful vectors

def helpful_vectors(BB, modulus):
    nothelpful = 0
    for ii in range(BB.dimensions()[0]):
        if BB[ii,ii] >= modulus:
            nothelpful += 1

​    print(nothelpful, "/", BB.dimensions()[0], " vectors are not helpful")

# display matrix picture with 0 and X

def matrix_overview(BB, bound):
    for ii in range(BB.dimensions()[0]):
        a = ('%02d ' % ii)
        for jj in range(BB.dimensions()[1]):
            a += '0' if BB[ii,jj] == 0 else 'X'
            if BB.dimensions()[0] < 60:
                a += ' '
        if BB[ii, ii] >= bound:
            a += '~'
        print(a)

# tries to remove unhelpful vectors

# we start at current = n-1 (last vector)

def remove_unhelpful(BB, monomials, bound, current):

    # end of our recursive function

​    if current == -1 or BB.dimensions()[0] <= dimension_min:
​        return BB

    # we start by checking from the end

​    for ii in range(current, -1, -1):

        # if it is unhelpful:

​        if BB[ii, ii] >= bound:
​            affected_vectors = 0
​            affected_vector_index = 0

            # let's check if it affects other vectors

​            for jj in range(ii + 1, BB.dimensions()[0]):

                # if another vector is affected:

                # we increase the count

​                if BB[jj, ii] != 0:
​                    affected_vectors += 1
​                    affected_vector_index = jj
​    

            # level:0

            # if no other vectors end up affected

            # we remove it

​            if affected_vectors == 0:
​                print("* removing unhelpful vector", ii)
​                BB = BB.delete_columns([ii])
​                BB = BB.delete_rows([ii])
​                monomials.pop(ii)
​                BB = remove_unhelpful(BB, monomials, bound, ii-1)
​                return BB
​    

            # level:1

            # if just one was affected we check

            # if it is affecting someone else

​            elif affected_vectors == 1:
​                affected_deeper = True
​                for kk in range(affected_vector_index + 1, BB.dimensions()[0]):

                    # if it is affecting even one vector

                    # we give up on this one

​                    if BB[kk, affected_vector_index] != 0:
​                        affected_deeper = False

                # remove both it if no other vector was affected and

                # this helpful vector is not helpful enough

                # compared to our unhelpful one

​                if affected_deeper and abs(bound - BB[affected_vector_index, affected_vector_index]) < abs(bound - BB[ii, ii]):
​                    print("* removing unhelpful vectors", ii, "and", affected_vector_index)
​                    BB = BB.delete_columns([affected_vector_index, ii])
​                    BB = BB.delete_rows([affected_vector_index, ii])
​                    monomials.pop(affected_vector_index)
​                    monomials.pop(ii)
​                    BB = remove_unhelpful(BB, monomials, bound, ii-1)
​                    return BB

    # nothing happened

​    return BB

""" 
Returns:

* 0,0   if it fails

* -1,-1 if `strict=true`, and determinant doesn't bound

* x0,y0 the solutions of `pol`
  """
  def boneh_durfee(pol, modulus, mm, tt, XX, YY):
    """
    Boneh and Durfee revisited by Herrmann and May

    finds a solution if:

    * d < N^delta
    * |x| < e^delta
    * |y| < e^0.5
      whenever delta < 1 - sqrt(2)/2 ~ 0.292
        """

    # substitution (Herrman and May)

    PR.<u, x, y> = PolynomialRing(ZZ)
    Q = PR.quotient(x*y + 1 - u) # u = xy + 1
    polZ = Q(pol).lift()

    UU = XX*YY + 1

    # x-shifts

    gg = []
    for kk in range(mm + 1):
        for ii in range(mm - kk + 1):
            xshift = x^ii * modulus^(mm - kk) * polZ(u, x, y)^kk
            gg.append(xshift)
    gg.sort()

    # x-shifts list of monomials

    monomials = []
    for polynomial in gg:
        for monomial in polynomial.monomials():
            if monomial not in monomials:
                monomials.append(monomial)
    monomials.sort()

    # y-shifts (selected by Herrman and May)

    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            yshift = y^jj * polZ(u, x, y)^kk * modulus^(mm - kk)
            yshift = Q(yshift).lift()
            gg.append(yshift) # substitution

    # y-shifts list of monomials

    for jj in range(1, tt + 1):
        for kk in range(floor(mm/tt) * jj, mm + 1):
            monomials.append(u^kk * y^jj)

    # construct lattice B

    nn = len(monomials)
    BB = Matrix(ZZ, nn)
    for ii in range(nn):
        BB[ii, 0] = gg[ii](0, 0, 0)
        for jj in range(1, ii + 1):
            if monomials[jj] in gg[ii].monomials():
                BB[ii, jj] = gg[ii].monomial_coefficient(monomials[jj]) * monomials[jj](UU,XX,YY)

    # Prototype to reduce the lattice

    if helpful_only:

        # automatically remove

  ​      BB = remove_unhelpful(BB, monomials, modulus^mm, nn-1)

        # reset dimension

  ​      nn = BB.dimensions()[0]
  ​      if nn == 0:
  ​          print("failure")
  ​          return 0,0

    # check if vectors are helpful

    if debug:
        helpful_vectors(BB, modulus^mm)

    # check if determinant is correctly bounded

    det = BB.det()
    bound = modulus^(mm*nn)
    if det >= bound:
        print("We do not have det < bound. Solutions might not be found.")
        print("Try with highers m and t.")
        if debug:
            diff = (log(det) - log(bound)) / log(2)
            print("size det(L) - size e^(m*n) = ", floor(diff))
        if strict:
            return -1, -1
    else:
        print("det(L) < e^(m*n) (good! If a solution exists < N^delta, it will be found)")

    # display the lattice basis

    if debug:
        matrix_overview(BB, modulus^mm)

    # LLL

    if debug:
        print("optimizing basis of the lattice via LLL, this can take a long time")

    BB = BB.LLL()

    if debug:
        print("LLL is done!")

    # transform vector i & j -> polynomials 1 & 2

    if debug:
        print("looking for independent vectors in the lattice")
    found_polynomials = False

    for pol1_idx in range(nn - 1):
        for pol2_idx in range(pol1_idx + 1, nn):

            # for i and j, create the two polynomials

  ​          PR.<w,z> = PolynomialRing(ZZ)
  ​          pol1 = pol2 = 0
  ​          for jj in range(nn):
  ​              pol1 += monomials[jj](w*z+1,w,z) * BB[pol1_idx, jj] / monomials[jj](UU,XX,YY)
  ​              pol2 += monomials[jj](w*z+1,w,z) * BB[pol2_idx, jj] / monomials[jj](UU,XX,YY)

            # resultant

  ​          PR.<q> = PolynomialRing(ZZ)
  ​          rr = pol1.resultant(pol2)
  ​    

            # are these good polynomials?

  ​          if rr.is_zero() or rr.monomials() == [1]:
  ​              continue
  ​          else:
  ​              print("found them, using vectors", pol1_idx, "and", pol2_idx)
  ​              found_polynomials = True
  ​              break
  ​      if found_polynomials:
  ​          break

    if not found_polynomials:
        print("no independant vectors could be found. This should very rarely happen...")
        return 0, 0

    rr = rr(q, q)

    # solutions

    soly = rr.roots()

    if len(soly) == 0:
        print("Your prediction (delta) is too small")
        return 0, 0

    soly = soly[0][0]
    ss = pol1(q, soly)
    solx = ss.roots()[0][0]

    #
    return solx, soly

def example():
    ############################################

    # How To Use This Script

​    ##########################################

​    #

    # The problem to solve (edit the following values)

​    #
​    

    # the modulus

​    N = 107505436651153972868256172927458682863384962980950626300023016225072477035531962210081972740487894427658040878262205693734911880215972363343499849037411996091935215324499998500280001539069563664673471788918797180228775246203241297837846844704493266809513512780251834022988415242950525647295962207347676276159

    # the public exponent

​    e = 46483493180168456907876964472003342599505589423824575610973682748466876137876722746536417805454147792987530564436875226141952843276430892859209813871491418332469407742523023206446900477888407552315053106617523965303933309326359897043169707586465120984991379773865649114063608940450932600749494216244527815359


    # the hypothesis on the private exponent (the theoretical maximum is 0.292)

​    delta = .276 # this means that d < N^delta
​    
​    #

    # Lattice (tweak those values)

​    #
​    

    # you should tweak this (after a first run), (e.g. increment it until a solution is found)

​    m = 8 # size of the lattice (bigger the better/slower)
​    

    # you need to be a lattice master to tweak these

​    t = int((1-2*delta) * m)  # optimization from Herrmann and May
​    X = 2*floor(N^delta)  # this _might_ be too much
​    Y = floor(N^(1/2))    # correct if p, q are ~ same size
​    
​    #

    # Don't touch anything below

​    #
​    

    # Problem put in equation

​    P.<x,y> = PolynomialRing(ZZ)
​    A = int((N+1)/2)
​    pol = 1 + x * (A + y)
​    
​    #

    # Find the solutions!

​    #
​    

    # Checking bounds

​    if debug:
​        print("=== checking values ===")
​        print("* delta:", delta)
​        print("* delta < 0.292", delta < 0.292)
​        print("* size of e:", int(log(e)/log(2)))
​        print("* size of N:", int(log(N)/log(2)))
​        print("* m:", m, ", t:", t)
​    

    # boneh_durfee

​    if debug:
​        print("=== running algorithm ===")
​        start_time = time.time()
​    
​    solx, soly = boneh_durfee(pol, e, m, t, X, Y)
​    

    # found a solution?

​    if solx > 0:
​        print("=== solution found ===")
​        if False:
​            print("x:", solx)
​            print("y:", soly)
​    
​        d = int(pol(solx, soly) / e)
​        print("private key found:", d)
​    else:
​        print("=== no solution was found ===")
​    
​    if debug:
​        print(("=== %s seconds ===" % (time.time() - start_time)))

if __name__ == "__main__":
    example()

这里观察到x是d1和d2的最大公因数

1
x = gcd(d1,d2)

求出x后u，v就很简单可以直接求出了

这里的hint知道是广义RSA

搜到这篇paper

根据论文中

论文给出了怎么求p，q是通过先求出p的近似值在打cooper求的

这里是先求出$\widehat{p+q}$ ,和$\widehat{p-q}$ 再将两式除2得到p̂,然后打cooper

这里论文中u，v好像是通过连分数展开r求得的，但是我试了一下好像没有得到（不知道是不是我理解错了），但是对这道题没有什影响

得到p后就是常规的RSA了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
from gmpy2 import mpz, sqrt, mpfr, get_context, is_prime, powmod

import random

from Crypto.Util.number import getPrime, GCD, bytes_to_long, inverse, long_to_bytes

import requests

from gmpy2 import mpz, sqrt, mpfr, get_context, is_prime, powmod

N1 = 7348121907179526913580177851026954330752768738291896096735058973559480119932817354982584848148959373549116865913413457772773261195054845650206020666330991

e3 = 23550626043318531686392597908767473613369638520090152127370654817423383818034484441592543825793324637247596257173381762273905254049903422039592935871962187682259917270517329309332496277455914971819636329971254701142348560600765095893262007065327568577225527780321485212099754825195447682395092115782178271206767089362177657624379873520519398661669609981034432208973165597218334711366939977911593062941916527006025062935544853270685363226130039339985009309168493915830639441795502226746782561939904234398557509011544985054339634943750567054335128439233603858646704023191283512166289385748291358620388592170413196949907

d1 = 1285707407708336469611922789424965876916577005852352154890635610024931952186455505

d2 = 1649010712229782299850848551980277578291258538000633837589698050054193337459137087

flag_ct = 3304275694820454674685997231149613707569155279977829020394149986905099581809908257209756187158847732534210083918959247704733651870464045546533643246315075

x = gmpy2.gcd(d1,d2)

print(x)

\#这里x是最大的公因数，求出u,v

v_and_u = d1 // x  

v_sub_u = d2 // x  

v, u = (v_and_u + v_sub_u) // 2, (v_and_u - v_sub_u) // 2  

print(v,u)

p_and_q = floor(sqrt(abs(2 * N1 + sqrt((N1^2 + 1)^2 - (e3 * u) / v))))

p_sub_q = floor(sqrt(abs(-2 * N1 + sqrt((N1^2 + 1)^2 - (e3 * u) / v))))

p0 = 115498994696631776334354360421501383036996098182355289461602274761923389881332

R.<x> = Zmod(N1)[]

f = x + p0

f = f.monic()

pad = f.small_roots(X = 2^16, beta = 0.4)

p = ZZ(p0 + pad[0])

q = N1 // p

phi = (p - 1) * (q - 1)

d = inverse_mod(e3, phi)

m = pow(flag_ct, d, N1)

print(long_to_bytes(m).decode())

Deadsec CTF2024 Raul Rosas

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
from Crypto.Util.number import * 

from sympy import nextprime

p1 = bin(getPrime(1024))[2:]

p2 = p1[:605]       419

p2 = p2 + ('0'*(len(p1)-len(p2)))

p1 = int(p1,2)

p2 = nextprime(int(p2,2))

q1 = getPrime(300)

q2 = getPrime(300)

n1 = p1*p1*q1 

n2 = p2*p2*q2 

e = 65537 

flag = bytes_to_long(b'REDACTED')

c1 = pow(flag,e,n1)

c2 = pow(flag,e,n2)

print(f'{n1=}')

print(f'{n2=}')

print(f'{c1=}')

print(f'{c2=}')

"""

n1=33914684861748025775039281034732118800210172226202865626649257734640860626122496857824722482435571212266837521062975265470108636677204118801674455876175256919094583111702086440374440069720564836535455468886946320281180036997133848753476194808776154286740338853149382219104098930424628379244203425638143586895732678175237573473771798480275214400819978317207532566320561087373402673942574292313462136068626729114505686759701305592972367260477978324301469299251420212283758756993372112866755859599750559165005003201133841030574381795101573167606659158769490361449603797836102692182242091338045317594471059984757228202609971840405638858696334676026230362235521239830379389872765912383844262135900613776738814453

n2=45676791074605066998943099103364315794006332282441283064976666268034083630735700946472676852534025506807314001461603559827433723291528233236210007601454376876234611894686433890588598497194981540553814858726066215204034517808726230108550384400665772370055344973309767254730566845236167460471232855535131280959838577294392570538301153645042892860893604629926657287846345355440026453883519493151299226289819375073507978835796436834205595029397133882344120359631326071197504087811348353107585352525436957117561997040934067881585416375733220284897170841715716721313708208669285280362958902914780961119036511592607473063247721427765849962400322051875888323638189434117452309193654141881914639294164650898861297303

c1=5901547799381070840359392038174495588170513247847714273595411167296183629412915012222227027356430642556122066895371444948863326101566394976530551223412292667644441453331065752759544619792554573114517925105448879969399346787436142706971884168511458472259984991259195488997495087540800463362289424481986635322685691583804462882482621269852340750338483349943910768394808039522826196641550659069967791745064008046300108627004744686494254057929843770761235779923141642086541365488201157760211440185514437408144860842733403640608261720306139244013974182714767738134497204545868435961883422098094282377180143072849852529146164709312766146939608395412424617384059645917698095750364523710239164016515753752257367489

c2=3390569979784056878736266202871557824004856366694719533085092616630555208111973443587439052592998102055488632207160968490605754861061546019836966349190018267098889823086718042220586285728994179393183870155266933282043334755304139243271973119125463775794806745935480171168951943663617953860813929121178431737477240925668994665543833309966378218572247768170043609879504955562993281112055931542971553613629203301798161781786253559679002805820092716314906043601765180455118897800232982799905604384587625502913096329061269176369601390578862509347479694697409545495592160695530037113884443071693090949908858172105089597051790694863761129626857737468493438459158669342430468741236573321658187309329276080990875017

"""

题目不难读懂，感觉有很多奇技淫巧来解

首先来审计代码，这里的代码十分简洁

给我们p1是一个1024bit的数，并且将其转为二进制

然后p2是取p1前419位，后面空出的位数用0来补齐

接着取p2的下一个素数

q1，q2的数量级都是300bit

最后给出了n1，n2 n1 = p12 * q1

n2 = p22 * q2

因为这里的p2是取p1的前419位，所以n1，n2大概也是相近的

所以用连分数展开 $$ \frac{n1}{n2} \approx \frac{q1}{q2} $$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
n1=33914684861748025775039281034732118800210172226202865626649257734640860626122496857824722482435571212266837521062975265470108636677204118801674455876175256919094583111702086440374440069720564836535455468886946320281180036997133848753476194808776154286740338853149382219104098930424628379244203425638143586895732678175237573473771798480275214400819978317207532566320561087373402673942574292313462136068626729114505686759701305592972367260477978324301469299251420212283758756993372112866755859599750559165005003201133841030574381795101573167606659158769490361449603797836102692182242091338045317594471059984757228202609971840405638858696334676026230362235521239830379389872765912383844262135900613776738814453

n2=45676791074605066998943099103364315794006332282441283064976666268034083630735700946472676852534025506807314001461603559827433723291528233236210007601454376876234611894686433890588598497194981540553814858726066215204034517808726230108550384400665772370055344973309767254730566845236167460471232855535131280959838577294392570538301153645042892860893604629926657287846345355440026453883519493151299226289819375073507978835796436834205595029397133882344120359631326071197504087811348353107585352525436957117561997040934067881585416375733220284897170841715716721313708208669285280362958902914780961119036511592607473063247721427765849962400322051875888323638189434117452309193654141881914639294164650898861297303

cf = continued_fraction(Integer(n1) / Integer(n2))

for i in range(2,2000):

  q1 = int(cf.numerator(i))    #获取连分数的分子

  q2 = int(cf.denominator(i))

  if n1 % q1 == 0 or n2 % q2 == 0:

    print(q1,q2)

    break

这样就得到了q1和q2

1
q1,q2 = 1226422900699937313306345486827490610540478397988332672940596868693721441368094739238893997,1651764208712002362909070586532659043033781575172011989418709627827265240039573208353001543

接下来就是解RSA了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import gmpy2

from Crypto.Util.number import *

q1,q2 = 1226422900699937313306345486827490610540478397988332672940596868693721441368094739238893997,1651764208712002362909070586532659043033781575172011989418709627827265240039573208353001543

 

e= 65537

c1=5901547799381070840359392038174495588170513247847714273595411167296183629412915012222227027356430642556122066895371444948863326101566394976530551223412292667644441453331065752759544619792554573114517925105448879969399346787436142706971884168511458472259984991259195488997495087540800463362289424481986635322685691583804462882482621269852340750338483349943910768394808039522826196641550659069967791745064008046300108627004744686494254057929843770761235779923141642086541365488201157760211440185514437408144860842733403640608261720306139244013974182714767738134497204545868435961883422098094282377180143072849852529146164709312766146939608395412424617384059645917698095750364523710239164016515753752257367489

n1=33914684861748025775039281034732118800210172226202865626649257734640860626122496857824722482435571212266837521062975265470108636677204118801674455876175256919094583111702086440374440069720564836535455468886946320281180036997133848753476194808776154286740338853149382219104098930424628379244203425638143586895732678175237573473771798480275214400819978317207532566320561087373402673942574292313462136068626729114505686759701305592972367260477978324301469299251420212283758756993372112866755859599750559165005003201133841030574381795101573167606659158769490361449603797836102692182242091338045317594471059984757228202609971840405638858696334676026230362235521239830379389872765912383844262135900613776738814453

p1 = gmpy2.iroot(n1//q1,2)[0]

d1 = gmpy2.invert(e, p1*(p1-1)*(q1-1))

m1 = pow(c1,d1,n1)

print(long_to_bytes(m1))

还有个是用二元cooper来打的 n2 = p22 * q2 = (x * 2605 + plow)2 * y

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
from Crypto.Util.number import *

import gmpy2

import itertools

def small_roots(f, bounds, m=1, d=None):

 if not d:

 d = f.degree()

 print(d)

 R = f.base_ring()

 N = R.cardinality()

 f /= f.coefficients().pop(0)

 f = f.change_ring(ZZ)

 G = Sequence([], f.parent())

 for i in range(m + 1):

 base = N ^ (m - i) * f ^ i

 for shifts in itertools.product(range(d), repeat=f.nvariables()):

  g = base * prod(map(power, f.variables(), shifts))

  G.append(g)

 B, monomials = G.coefficient_matrix()

 monomials = vector(monomials)

 factors = [monomial(*bounds) for monomial in monomials]

 for i, factor in enumerate(factors):

 B.rescale_col(i, factor)

 B = B.dense_matrix().LLL()

 B = B.change_ring(QQ)

 for i, factor in enumerate(factors):

 B.rescale_col(i, 1 / factor)

 H = Sequence([], f.parent().change_ring(QQ))

 for h in filter(None, B * monomials):

 H.append(h)

 I = H.ideal()

 if I.dimension() == -1:

  H.pop()

 elif I.dimension() == 0:

  roots = []

  for root in I.variety(ring=ZZ):

  root = tuple(R(root[var]) for var in f.variables())

  roots.append(root)

  return roots

 return []

n2=45676791074605066998943099103364315794006332282441283064976666268034083630735700946472676852534025506807314001461603559827433723291528233236210007601454376876234611894686433890588598497194981540553814858726066215204034517808726230108550384400665772370055344973309767254730566845236167460471232855535131280959838577294392570538301153645042892860893604629926657287846345355440026453883519493151299226289819375073507978835796436834205595029397133882344120359631326071197504087811348353107585352525436957117561997040934067881585416375733220284897170841715716721313708208669285280362958902914780961119036511592607473063247721427765849962400322051875888323638189434117452309193654141881914639294164650898861297303

c2=3390569979784056878736266202871557824004856366694719533085092616630555208111973443587439052592998102055488632207160968490605754861061546019836966349190018267098889823086718042220586285728994179393183870155266933282043334755304139243271973119125463775794806745935480171168951943663617953860813929121178431737477240925668994665543833309966378218572247768170043609879504955562993281112055931542971553613629203301798161781786253559679002805820092716314906043601765180455118897800232982799905604384587625502913096329061269176369601390578862509347479694697409545495592160695530037113884443071693090949908858172105089597051790694863761129626857737468493438459158669342430468741236573321658187309329276080990875017

for p_lo in tqdm(range(1, 2000)):

  R = Integers(n)

  P.<x, y> = PolynomialRing(R)

  sz = 1024-605

  f = (x * (2^sz) + p_lo)^2 * (y + 2^299)

  bounds = (2^(1024-sz), 2^298)

  roots = small_roots(f, bounds)[0]

  p_hi = int(roots[0])

  p = p_hi*(2^sz) + int(p_lo)

  p = int(p)

  n = int(n)

  if GCD(p, n) > 1:

​    print(p_lo)

​    print(p)

​    assert is_prime(p)

​    q = n // (p*p)

​    phi = p * (p - 1) * (q - 1)

​    d = pow(65537, -1, phi)

​    m = pow(c2, d, n)

​    print(long_to_bytes(int(m)))

​    break

idekCTF 2025 Diamond Ticket

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
from Crypto.Util.number import *

#Some magic from Willy Wonka
p = 170829625398370252501980763763988409583
a = 164164878498114882034745803752027154293
b = 125172356708896457197207880391835698381

def chocolate_generator(m:int) -> int:
    return (pow(a, m, p) + pow(b, m, p)) % p

#The diamond ticket is hiding inside chocolate
diamond_ticket = open("flag.txt", "rb").read()
assert len(diamond_ticket) == 26
assert diamond_ticket[:5] == b"idek{"
assert diamond_ticket[-1:] == b"}"
diamond_ticket = bytes_to_long(diamond_ticket[5:-1])

flag_chocolate = chocolate_generator(diamond_ticket)
chocolate_bag = []

#Willy Wonka are making chocolates
for i in range(1337):
    chocolate_bag.append(getRandomRange(1, p))

#And he put the golden ticket at the end
chocolate_bag.append(flag_chocolate)

#Augustus ate lots of chocolates, but he can't eat all cuz he is full now :D
remain = chocolate_bag[-5:]

#Compress all remain chocolates into one
remain_bytes = b"".join([c.to_bytes(p.bit_length()//8, "big") for c in remain])

#The last chocolate is too important, so Willy Wonka did magic again
P = getPrime(512)
Q = getPrime(512)
N = P * Q
e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}")
d = pow(e, -1, (P - 1) * (Q - 1))
c1 = pow(bytes_to_long(remain_bytes), e, N)
c2 = pow(bytes_to_long(remain_bytes), 2, N) # A small gift

#How can you get it ?
print(f"{N = }")
print(f"{c1 = }")
print(f"{c2 = }") 

"""
N = 85494791395295332945307239533692379607357839212287019473638934253301452108522067416218735796494842928689545564411909493378925446256067741352255455231566967041733698260315140928382934156213563527493360928094724419798812564716724034316384416100417243844799045176599197680353109658153148874265234750977838548867
c1 = 27062074196834458670191422120857456217979308440332928563784961101978948466368298802765973020349433121726736536899260504828388992133435359919764627760887966221328744451867771955587357887373143789000307996739905387064272569624412963289163997701702446706106089751532607059085577031825157942847678226256408018301
c2 = 30493926769307279620402715377825804330944677680927170388776891152831425786788516825687413453427866619728035923364764078434617853754697076732657422609080720944160407383110441379382589644898380399280520469116924641442283645426172683945640914810778133226061767682464112690072473051344933447823488551784450844649
"""

idekCTF 2025 - Giap’s Blog

这里出题人的wp

首先是题目给出了一个自定义函数,我们还知道其中a,b,p的值

1
2
def chocolate_generator(m:int) -> int:
    return (pow(a, m, p) + pow(b, m, p)) % p

然后给出一下的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#The diamond ticket is hiding inside chocolate
diamond_ticket = open("flag.txt", "rb").read()
assert len(diamond_ticket) == 26
assert diamond_ticket[:5] == b"idek{"
assert diamond_ticket[-1:] == b"}"
diamond_ticket = bytes_to_long(diamond_ticket[5:-1])

flag_chocolate = chocolate_generator(diamond_ticket)
chocolate_bag = []

#Willy Wonka are making chocolates
for i in range(1337):
    chocolate_bag.append(getRandomRange(1, p))

#And he put the golden ticket at the end
chocolate_bag.append(flag_chocolate)

#Augustus ate lots of chocolates, but he can't eat all cuz he is full now :D
remain = chocolate_bag[-5:]

#Compress all remain chocolates into one
remain_bytes = b"".join([c.to_bytes(p.bit_length()//8, "big") for c in remain])

生成1337个随机数，其中范围是(1，p)然后存入chocolate_bag中

再将flag_chocolate加入chocolate_bag的末尾

remain是取chocolate_bag的最后五位数，然后将这个五个元素拼接为字节串

接着又是一个新的加密

1
2
3
4
5
6
7
P = getPrime(512)
Q = getPrime(512)
N = P * Q
e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}")
d = pow(e, -1, (P - 1) * (Q - 1))
c1 = pow(bytes_to_long(remain_bytes), e, N)
c2 = pow(bytes_to_long(remain_bytes), 2, N) # A small gift

这里很明显用共模攻击可以直接打，那么可以恢复出remain_bytes

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from Crypto.Util.number import *

N = 85494791395295332945307239533692379607357839212287019473638934253301452108522067416218735796494842928689545564411909493378925446256067741352255455231566967041733698260315140928382934156213563527493360928094724419798812564716724034316384416100417243844799045176599197680353109658153148874265234750977838548867
c1 = 27062074196834458670191422120857456217979308440332928563784961101978948466368298802765973020349433121726736536899260504828388992133435359919764627760887966221328744451867771955587357887373143789000307996739905387064272569624412963289163997701702446706106089751532607059085577031825157942847678226256408018301
c2 = 30493926769307279620402715377825804330944677680927170388776891152831425786788516825687413453427866619728035923364764078434617853754697076732657422609080720944160407383110441379382589644898380399280520469116924641442283645426172683945640914810778133226061767682464112690072473051344933447823488551784450844649

# e 是 b"idek{this_is_a_fake_flag_lolol}" 转成的整数

e = bytes_to_long(b"idek{this_is_a_fake_flag_lolol}")


# 扩展欧几里得算法求 a, b

def egcd(a, b):
    if b == 0:
        return (1, 0, a)
    x1, y1, g = egcd(b, a % b)
    return (y1, x1 - (a // b) * y1, g)

a, b, g = egcd(e, 2)

# 确保得到的是 e*a + 2*b = 1

assert e*a + 2*b == 1

# 如果有负数指数，要取模逆

if a < 0:
    c1 = pow(c1, -1, N)
    a = -a
if b < 0:
    c2 = pow(c2, -1, N)
    b = -b

rb = (pow(c1, a, N) * pow(c2, b, N)) % N
remain_bytes = long_to_bytes(rb)[-16:]
flag_chocolate = bytes_to_long(remain_bytes)

print(flag_chocolate)

现在我们可以列出方程 c ≡ am + bm (mod  p) 我们不妨令b = ak,那么我们就有 c ≡ am + (ak)m (mod  p)

c ≡ am + (ak)m (mod  p)

现在再令X=a^m,那么就有方程 c ≡ X + Xk (mod  p) 解这个X的trick在这里

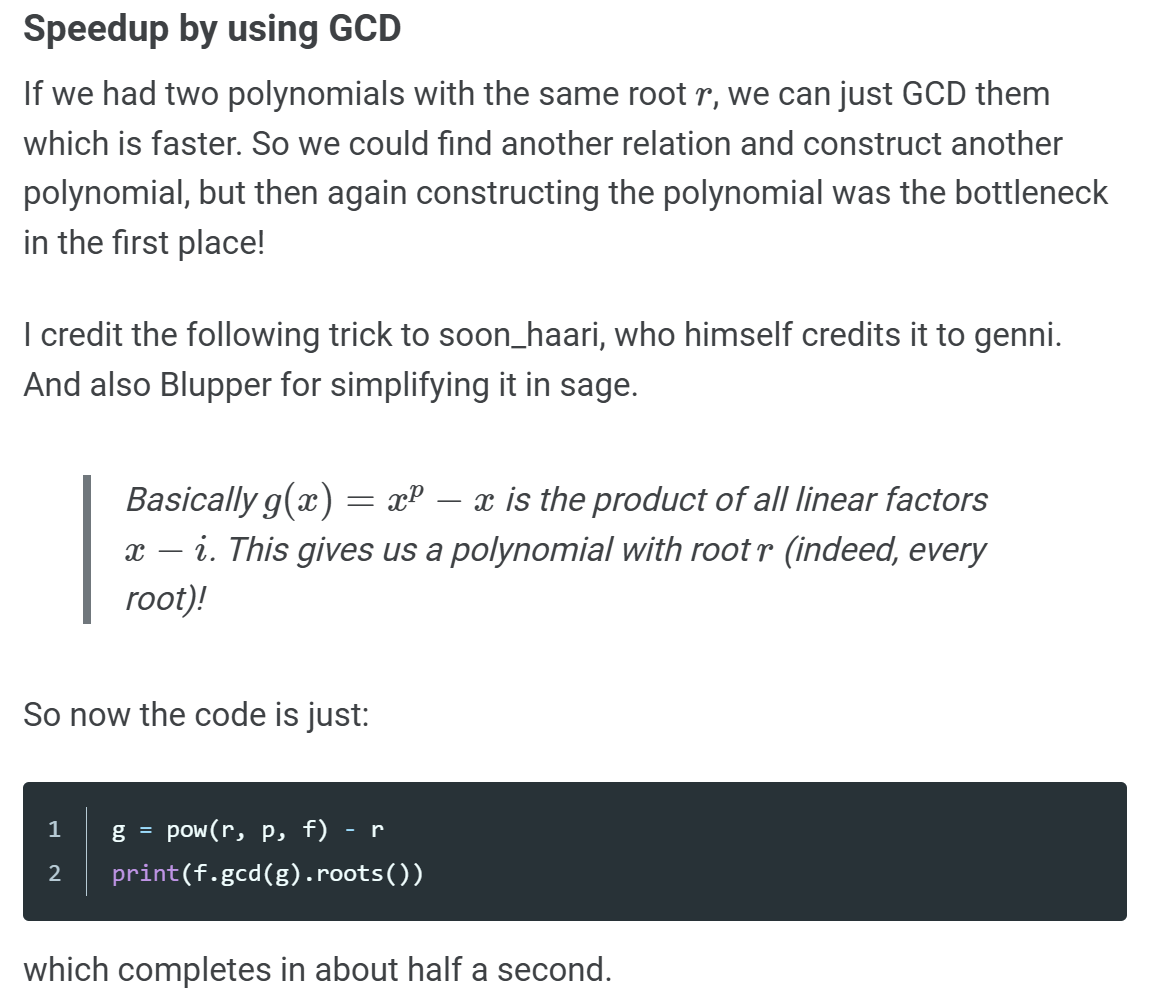
我们可以先求出k

1
2
3
4
5
6
7
8
9
10
11
12
13
p = 170829625398370252501980763763988409583

a = 164164878498114882034745803752027154293

b = 125172356708896457197207880391835698381

import sympy

k=sympy.discrete_log(p,b,a)

print(k)
#也可以直接用sage中的函数解
k = GF(p)(b).log(a)

根据上面的列出方程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
p = 170829625398370252501980763763988409583

a = 164164878498114882034745803752027154293

b = 125172356708896457197207880391835698381

c = 99584795316725433978492646071734128819


PR.<x> = PolynomialRing(GF(p))

f = x + x^k - c

g = pow(x, p, f) - x

print(f.gcd(g).roots())

然后就是在解一个离散对数

1
m = GF(p)(X).log(a)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
p = 170829625398370252501980763763988409583

a = 164164878498114882034745803752027154293

b = 125172356708896457197207880391835698381

c = 99584795316725433978492646071734128819

k = GF(p)(b).log(a)

print(k)

PR.<x> = PolynomialRing(GF(p))

f = x + x**k - c

g = pow(x, p, f) - x

X = [r for r in f.gcd(g).roots()][0][0]

m = GF(p)(X).log(a)

print(f'{m = }') # 4807895356063327854843653048517090061

这里求出的m是m%p后的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
load('https://raw.githubusercontent.com/TheBlupper/linineq/refs/heads/main/linineq.py')

p = 170829625398370252501980763763988409583
o = (p-1)//2
m = 4807895356063327854843653048517090061

M = matrix([[256**i for i in reversed(range(20))]])
b = [m]
lb = [30]*20 
ub = [128]*20 

for sol in solve_bounded_mod_gen(M, b, lb, ub, o, solver='ortools'):
    print(bytes(sol))

idekCTF 2024 Golden Ticket

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import *

#Some magic from Willy Wonka
def chocolate_generator(m:int) -> int:
    p = 396430433566694153228963024068183195900644000015629930982017434859080008533624204265038366113052353086248115602503012179807206251960510130759852727353283868788493357310003786807
    return (pow(13, m, p) + pow(37, m, p)) % p

#The golden ticket is hiding inside chocolate
flag = b"idek{REDACTED}"
golden_ticket = bytes_to_long(flag)
flag_chocolate = chocolate_generator(golden_ticket)
chocolate_bag = []

#Willy Wonka is making chocolates
for i in range(golden_ticket):
    chocolate_bag.append(chocolate_generator(i))

#And he put the golden ticket at the end
chocolate_bag.append(flag_chocolate)

#Augustus ate lots of chocolates, but he can't eat all cuz he is full now :D
remain = chocolate_bag[-2:]

#Can you help Charles get the golden ticket?
print(remain)

#[88952575866827947965983024351948428571644045481852955585307229868427303211803239917835211249629755846575548754617810635567272526061976590304647326424871380247801316189016325247, 67077340815509559968966395605991498895734870241569147039932716484176494534953008553337442440573747593113271897771706973941604973691227887232994456813209749283078720189994152242]

上题就是在这题的基础上进行改进

golden_ticket：将flag数值化后的结果 flag_chocolate = chocolate_generator(golden_ticket) p = 396430433566694153228963024068183195900644000015629930982017434859080008533624204265038366113052353086248115602503012179807206251960510130759852727353283868788493357310003786807 返回 (pow(13, golden_ticket, p) + pow(37, golden_ticket, p)) % p chocolate_bag = [] 对于0以上、golden_ticket未満的i，执行以下操作： 将chocolate_generator(i)添加到chocolate_bag中 将flag_chocolate添加到chocolate_bag中 remain: chocolate_bag的最后两个元素 输出remain

我们有

1
2
(x + y) % p = c1
(13 * x + 37 * y) % p = c2
$$ =

$$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import *

p = 396430433566694153228963024068183195900644000015629930982017434859080008533624204265038366113052353086248115602503012179807206251960510130759852727353283868788493357310003786807
c1 = 88952575866827947965983024351948428571644045481852955585307229868427303211803239917835211249629755846575548754617810635567272526061976590304647326424871380247801316189016325247
c2 = 67077340815509559968966395605991498895734870241569147039932716484176494534953008553337442440573747593113271897771706973941604973691227887232994456813209749283078720189994152242

A = matrix(Zmod(p), [[1, 1], [13, 37]])
C = matrix(Zmod(p), [[c1], [c2]])
X = ~A * C

x = X[0][0]
y = X[1][0]

X = matrix(Zmod(p), [[x], [y]])

R = IntegerModRing(p)
golden_ticket = int(discrete_log(R(y), R(37))) + 1
flag = long_to_bytes(golden_ticket).decode()
print(flag)

WHYCTF 2025

substituteteacher

1
2
3
4
5
6
7
8
9
"Lcb gpzs tpvcbx phpzsvl ewig lgbsmc mwpl, bpmc xgwj p lzse, mwtx pmmivplzws. Pswlcbg dzvvzsh jbgvws mpvb, pswlcbg xbpx bsx, pswlcbg dzvbgpytb Libvxpe. Xblbmlzub Dztbv Mwgyzs, lcpl'v ewi, psx ewig miggbsl tbpx (p mgejlzm, fplbg-xpdphbx swlb rwisx zs p jzhbws'v sbvl – xws'l pva) cpv ygwihcl ewi lw lcb bxhb wr lcb zsrpdwiv Gpubsfwwx Fwwxv. Twmptv fczvjbgbx lptbv wr vlgpshb tzhclv psx bubs vlgpshbg xzvpjjbpgpsmbv. 'Jgwypyte kivl p jpglzmitpgte phhgbvvzub ypxhbg,' ewi'x dillbgbx lw ewigvbtr, yil lcb isbpvb zs ewig hil lwtx p xzrrbgbsl vlwge.

Lcb jplc, zr ewi mwitx bubs mptt zl lcpl, xzvvwtubx zslw p dixxe, wubghgwfs lgpma. Pcbpx, ypgbte uzvzytb lcgwihc lcb xwfsjwig, p rpzsl rtzmabg wr tzhcl. P mpyzs. Fwwxbs, xztpjzxplbx, psx twwazsh tzab zl cpx vfpttwfbx dwgb lcps p rbf vbmgblv.

'Fbtt, Dztbv,' ewi vzhcbx, 'ewi'ub mbglpzste vbbs fwgvb zsuzlplzwsv lw lblpsiv.'

Ewi jivc wjbs lcb mgbpae fwwxbs xwwg. Lcb vdbtt wr xpdj bpglc psx vwdblczsh uphibte dblpttzm, tzab wtx jbsszbv, rzttv ewig swvlgztv. Pv ewi vlbj zsvzxb, p vixxbs, cbpue LCIX bmcwbv ybczsx ewi. Lcb xwwg vtpdv vcil. Ewi lge lcb cpsxtb. Twmabx. Psx sw pdwisl wr kzhhtzsh, gplltzsh, wg jwtzlb jtbpxzsh vbbdv lw dpab p xzrrbgbsmb.

"Ewi pgb zs p xzdte tzl, gbmlpshitpg gwwd. Lcb pzg zv lczma fzlc lcb vmbsl wr xpdj fwwx psx vwdblczsh isxbrzspytb, jbgcpjv kivl lcb tzshbgzsh xgbpx wr rwghwllbs tzubv. Gpzs vlgbpav xwfs lcb vzshtb, hgzde fzsxwf ws lcb rpg fptt. P mgixb fwwxbs lpytb, lfw gzmable mcpzgv, psx p xivle, dwlc-bplbs gih pgb lcb wste rigszligb. P vdptt, istzl rzgbjtpmb vzlv phpzsvl wsb fptt, zlv cbpglc rzttbx fzlc mwtx pvcbv. Ws lcb lpytb, p rtzmabgzsh wzt tpdj mpvlv xpsmzsh vcpxwfv. Sbql lw lcb tpdj tpev p swlbywwa fzlc lcb rwttwfzsh lbql vmgzyytbv ws zl: rtph{yx96xy352436br4r8bm6mpxp5979y038}."

直接用quipqiup解密即可得到

1
"The rain lashed against your trench coat, each drop a tiny, cold accusation. Another missing person case, another dead end, another miserable Tuesday. Detective Miles Corbin, that's you, and your current lead (a cryptic, water-damaged note found in a pigeon's nest – don't ask) has brought you to the edge of the infamous Ravenwood Woods. Locals whispered tales of strange lights and even stranger disappearances. 'Probably just a particularly aggressive badger,' you'd muttered to yourself, but the unease in your gut told a different story. The path, if you could even call it that, dissolved into a muddy, overgrown track. Ahead, barely visible through the downpour, a faint flicker of light. A cabin. Wooden, dilapidated, and looking like it had swallowed more than a few secrets. 'Well, Miles,' you sighed, 'you've certainly seen worse invitations to tetanus.' You push open the creaky wooden door. The smell of damp earth and something vaguely metallic, like old pennies, fills your nostrils. As you step inside, a sudden, heavy THUD echoes behind you. The door slams shut. You try the handle. Locked. And no amount of jiggling, rattling, or polite pleading seems to make a difference. "You are in a dimly lit, rectangular room. The air is thick with the scent of damp wood and something undefinable, perhaps just the lingering dread of forgotten lives. Rain streaks down the single, grimy window on the far wall. A crude wooden table, two rickety chairs, and a dusty, moth-eaten rug are the only furniture. A small, unlit fireplace sits against one wall, its hearth filled with cold ashes. On the table, a flickering oil lamp casts dancing shadows. Next to the lamp lays a notebook with the following text scribbles on it: flag{bd96db352436ef4f8ec6cada5979b038}."

somkracht65537

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
from Crypto.Util.number import *

p = getPrime(1024)

q = getPrime(1024)

N = p*q

e = 65537

msg = bytes_to_long(b"flag{dummy_flag}")

ct1 = pow(msg, e, N)

ct2 = pow(msg, p+q, N)

print(f"{N = }")

print(f"{ct1 = }")

print(f"{ct2 = }")

"""

N = 13172635138210286640933237746072073728198869440440273861514688422430115450596963502627269613634657978751692320585777768877613321668778514462972611542147278205792418292362109100597755668571861738781190210255903465162483813897653948305531342676537057130369323555420200545974179860718822410192595079238246216026529376260568656408216009127973127738250617629330070723654601189310430802429585919291621479622419163092371272056180409609142738265178224163465585013019636286435078812898907472859171136422659050412212315590509027225331104292443193693974638004592849794819591007103879538185323581422819852185166422985403024630123

ct1 = 8499526321488266762028127474977263983474334713646962923180757984708039537289636737028409522654349845032612940144246996001396064450188534247830979105036627472087587636695469693411422088223080856169980341928057477564688506588678465277896123712776169270866525885072607021419929184184301722442524104467963680432737243478200661224741027413690099507128782156810842444314483076587935222998920241102484844741597333281611874849648935849985954902264102662618041817365284648356127737145896858259709819593359264714426125676691235985164360773645489923563993927995838346085066937602961724919392025887999986486672200850129835569774

ct2 = 2263178005282615069738169250508811825030372342139636879043114251227029802177975391784856426659871916802959302578620910469427367218786299839311310420522660987052055310279591316813828952756984548230575321772825193775083404279028090110850848262192595930920326368607665856808251531130234210906413358662814500632504899088517752958423466186872534450108628371006268110210630017230741670440780982809417986017372337888735465439382827207990030719121834402226087906249993820193417658352914727984318783025375497623944699995700474418221251293446038111913247755996471673024017921092527032486774115935601292346440934530921157935322

"""

题目十分简洁

1
2
3
ct1 = pow(msg, e, N)

ct2 = pow(msg, p+q, N)

这样的式子一看就是可以打共模攻击的，但是这里p+q的值不知道

由欧拉定理可以知道

如果gcd(m,N)=1 mφ(N) ≡ 1 (mod  N) 对于任意整数 k有 ma ≡ ma + kφ(N) (mod  N) 指数可以加上（或减去）φ(N) 的倍数而不改变结果

这就是幂在 φ(N) 的周期性

那么知道这里后面就简单了 ct2 = msgp + q mod  N

ct2 = msgp + q + φ(N) mod  N

ct2 = msgp + q + (p * q − p − q + 1) mod  N

ct2 = msgN + 1 mod  N

接下来打个共模攻击就好

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import gmpy2

from Crypto.Util.number import *

def commom_modulus_attack(c1, c2, e1, e2, n):

  gcd, s1, s2 = gmpy2.gcdext(e1, e2)

  if s1 < 0:

    s1 = -s1

    c1 = gmpy2.invert(c1, n)

  elif s2 < 0:

    s2 = -s2

    c2 = gmpy2.invert(c2, n)

  v = pow(c1, s1, n)

  w = pow(c2, s2, n)

  x = (v*w) % n

  return x

e = 65537

N = 13172635138210286640933237746072073728198869440440273861514688422430115450596963502627269613634657978751692320585777768877613321668778514462972611542147278205792418292362109100597755668571861738781190210255903465162483813897653948305531342676537057130369323555420200545974179860718822410192595079238246216026529376260568656408216009127973127738250617629330070723654601189310430802429585919291621479622419163092371272056180409609142738265178224163465585013019636286435078812898907472859171136422659050412212315590509027225331104292443193693974638004592849794819591007103879538185323581422819852185166422985403024630123

ct1 = 8499526321488266762028127474977263983474334713646962923180757984708039537289636737028409522654349845032612940144246996001396064450188534247830979105036627472087587636695469693411422088223080856169980341928057477564688506588678465277896123712776169270866525885072607021419929184184301722442524104467963680432737243478200661224741027413690099507128782156810842444314483076587935222998920241102484844741597333281611874849648935849985954902264102662618041817365284648356127737145896858259709819593359264714426125676691235985164360773645489923563993927995838346085066937602961724919392025887999986486672200850129835569774

ct2 = 2263178005282615069738169250508811825030372342139636879043114251227029802177975391784856426659871916802959302578620910469427367218786299839311310420522660987052055310279591316813828952756984548230575321772825193775083404279028090110850848262192595930920326368607665856808251531130234210906413358662814500632504899088517752958423466186872534450108628371006268110210630017230741670440780982809417986017372337888735465439382827207990030719121834402226087906249993820193417658352914727984318783025375497623944699995700474418221251293446038111913247755996471673024017921092527032486774115935601292346440934530921157935322

e1 = e

e2 = N + 1

m = commom_modulus_attack(ct1, ct2, e1, e2, N)

flag = long_to_bytes(m).decode()

print(flag)