Shamir’s secret sharing算法

该算法由于Shamir提出，也就是RSA中的这S

算法概述：

秘密s被分成n份毫无相关的部分信息，每一部分信息称为一个子密钥，由一个参与者持有，只有至少拥有k份子密钥时才能恢复出秘密s，这种方案为(k, n)-秘密分割门限方案，k称为方案的门限值

一个秘密S要由n个人来保管

将s分为n个值→{s1, s2, s3,…,sn}

保证从中任取k个值,可以还原出s，{s1, s2, s3,…,sn}→s

保证从中任取k-1个值不能还原出s,{s1, s2, s3,…,sn}↛s

算法实现：

这是如何实现的呢

我们可以先回顾下多项式的性质

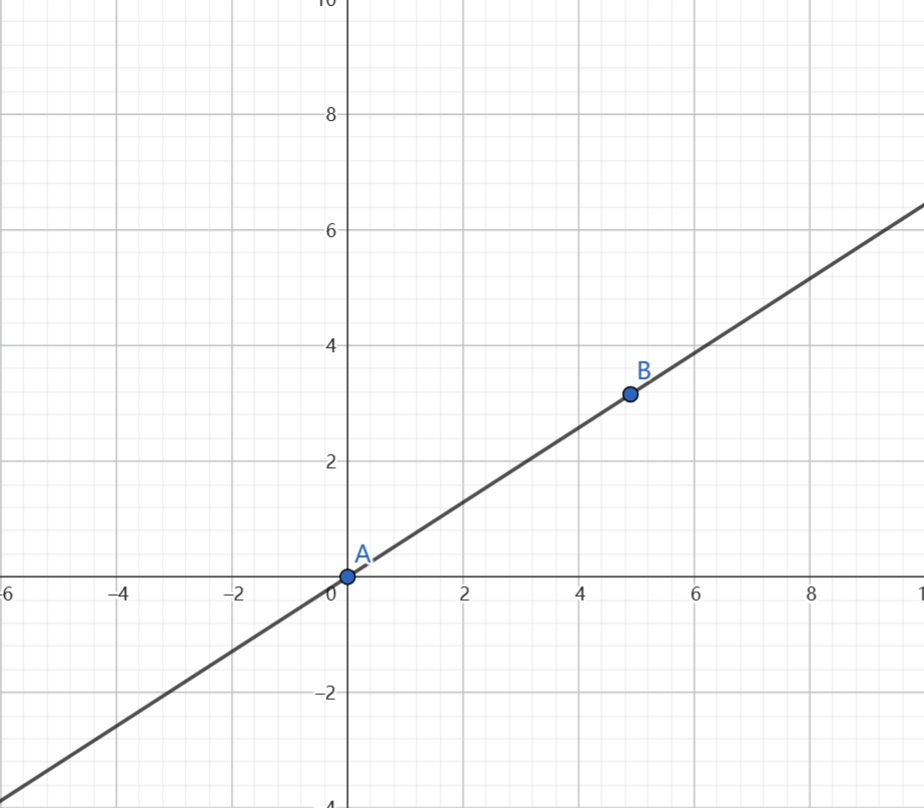
两个点可以确定唯一的一条直线也就是一次多项式

但是确不能确定唯一的二次多项式

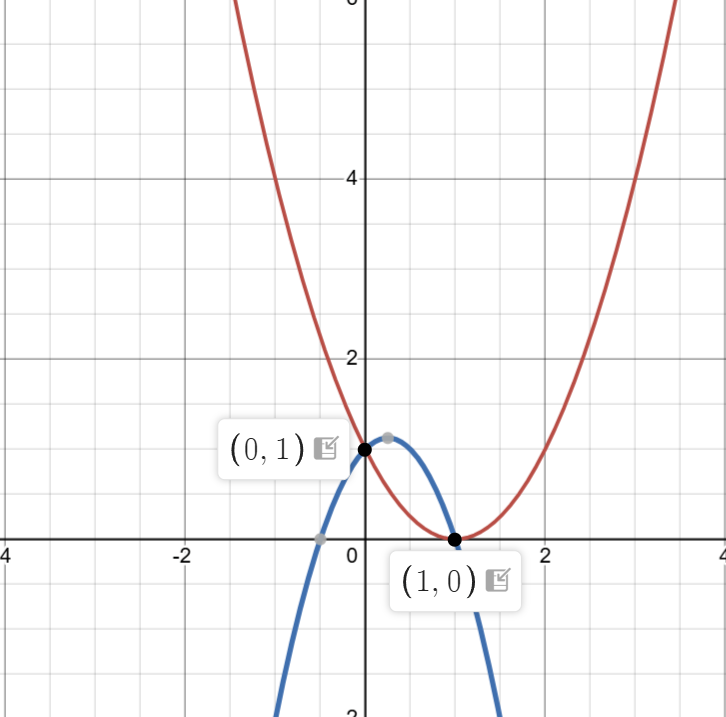
但是三个点就可以确定唯一的二次多项式

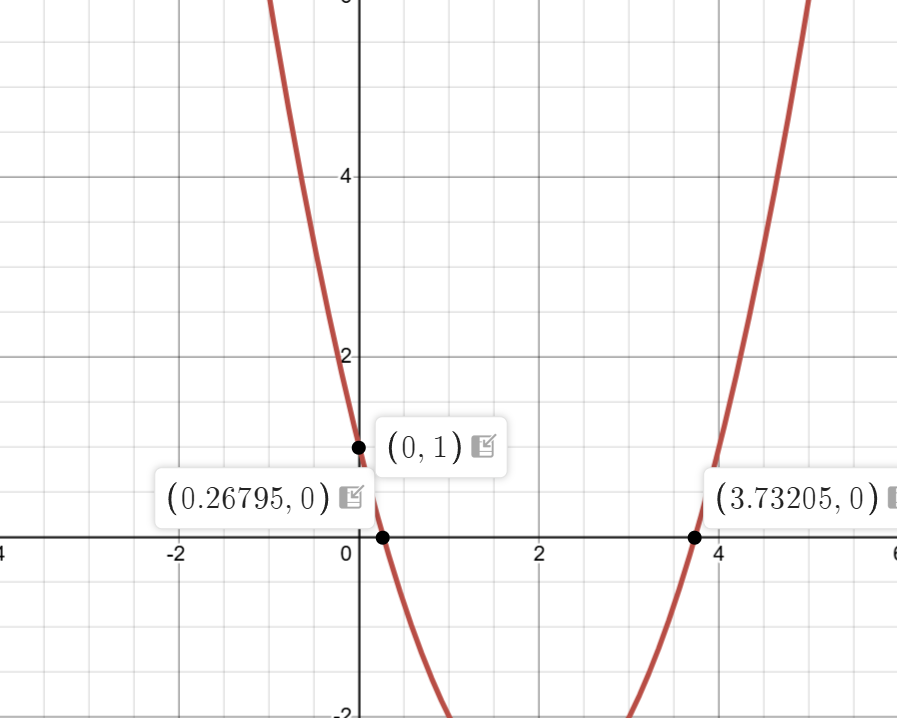
对结论推广，我们可以知道k-1次的多项式可以由k个点来唯一确定

回到算法中，我们将秘密看成是k-1次多项式我们可以得到 f(x) = S + a1x + a2x + … + ak − 1xk − 1 s作为秘密放入常数项中

为了避免数论方法的攻击，所以使用了有限域下的多项式 f(x) ≡ S + a1x + a2x + … + ak − 1xk − 1 (mod  P) 从中任意取n个数，n1, n2, ..., n3带入多项式计算，yi = f(xi)

将n个密钥对,(x1, f(x1)), (x2, f(x2), (x3, f(x3)), ..., (xn, f(xn)发给n个持有者

算法破解：

方法一：

任取n个密钥对代入求解多项式系数 a0 + a1x1 + ... + at − 1x1t − 1 = y1

a0 + a1x2 + ... + at − 1x2t − 1 = y2

...

a0 + a1xt + ... + at − 1xtt − 1 = yt

用矩阵乘法来表示 $$ \begin{pmatrix} 1 & x_1 & x_1^2 & \cdots & x_1^{t-1} \\ 1 & x_2 & x_2^2 & \cdots & x_2^{t-1} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_t & x_t^2 & \cdots & x_t^{t-1} \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_{t-1} \end{pmatrix} = \begin{pmatrix} y_1 \\ y_2 \\ \vdots \\ y_t \end{pmatrix} $$ 求得的a0即是原始的秘密

方法二：

我们可以用拉格朗日插值法来恢复系数 $$ (f(x) = \sum_{i=1}^{t} y_i \prod_{j=1,j\ne i}^{t} \frac{x - x_j}{x_i - x_j}) $$ 令x=0,求得s $$ s = \sum_{i=1}^t y_i \prod_{j=1,j\neq i}^t \frac{x_j}{x_j - x_i} $$

SSS

1
2
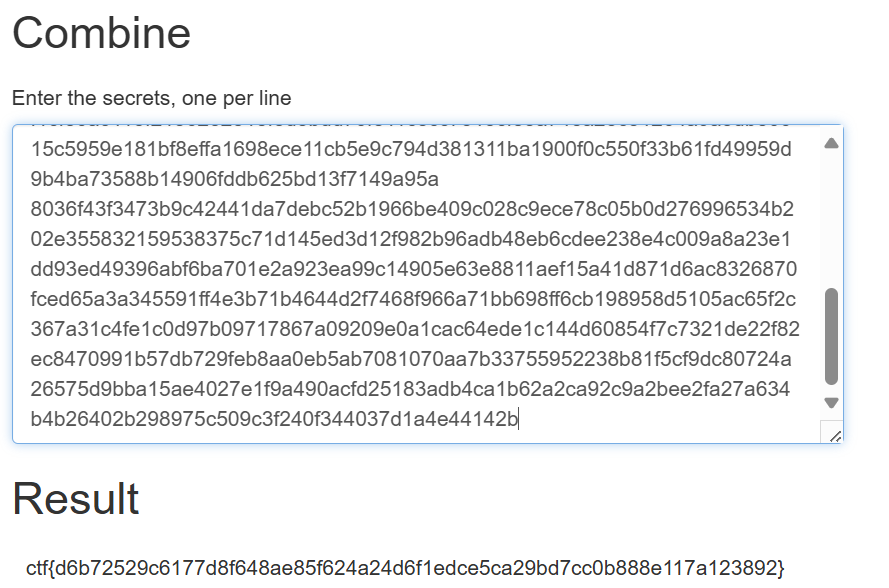
3
8010ba0d6ed38ef563074c3ee80a44f7fe680e82015a8d35f7f2245f66ec9c889b4e31a0c3e97bceeb6f28695f7a494918e0ca079677f07fff8eb570c17a4cb1db0477b84e9c68b9f02b21b33850f33bbd18f886b65c1f3bb015ddbe2723e64abfe8595e181d69d3f8ca3b7cc01c875ea25b97ef1e171c4f3f887e5752541270ae461cc610b3eb422c34df84e7b9a567f7933ee4b6969d19273d212a3ee92f8509679a4b40b6823c007e6d5c6241959e86bc8f989754649cd3008bdbb5bf030c9e802adf54d3afce4edef9bb709c7db4c2ac1f96f3e05cd220534b5647f35888e0e3d2435abdb1d7f32413bb630b3e8b0502e774dda8ac2bd4c2623ac433f79bd12
80264e325aa037314746964303cf6fee98d64e1e03d613fb8f327f5241850adbd06e1f959bdb6e5bd35874188e3fa4740a1948befcacb8949350574825ba4519793a6a617048fb2f5bdd9bc3267a61051484ec16e83ff7baaafac81a3aa4fb2077da312ee4f00c705b8f626334ff3045e41f451858988a3549e314f8a70f0879f5a30fbcd5fcc1645575186af8a434876304bb1ebc360533389143f7d918682307736bac713b63338482ef1cf80ac415f213625231ef3d3bdd70f811c8cc7515cf83a74ea25c31264a9a5dbe0615c5959e181bf8effa1698ece11cb5e9c794d381311ba1900f0c550f33b61fd49959d9b4ba73588b14906fddb625bd13f7149a95a
8036f43f3473b9c42441da7debc52b1966be409c028c9ece78c05b0d276996534b202e355832159538375c71d145ed3d12f982b96adb48eb6cdee238e4c009a8a23e1dd93ed49396abf6ba701e2a923ea99c14905e63e8811aef15a41d871d6ac8326870fced65a3a345591ff4e3b71b4644d2f7468f966a71bb698ff6cb198958d5105ac65f2c367a31c4fe1c0d97b09717867a09209e0a1cac64ede1c144d60854f7c7321de22f82ec8470991b57db729feb8aa0eb5ab7081070aa7b33755952238b81f5cf9dc80724a26575d9bba15ae4027e1f9a490acfd25183adb4ca1b62a2ca92c9a2bee2fa27a634b4b26402b298975c509c3f240f344037d1a4e44142b

有次比赛中只给了三个数据，当时看的时候一脸懵逼，后面看了其它师傅的博客发现有个在线网站可以解