ECC

椭圆曲线是什么

满足 Weierstrass 方程的点集,形如： Y2 = X3 + AX + B 这样的等式称为椭圆曲线(elliptic curve)

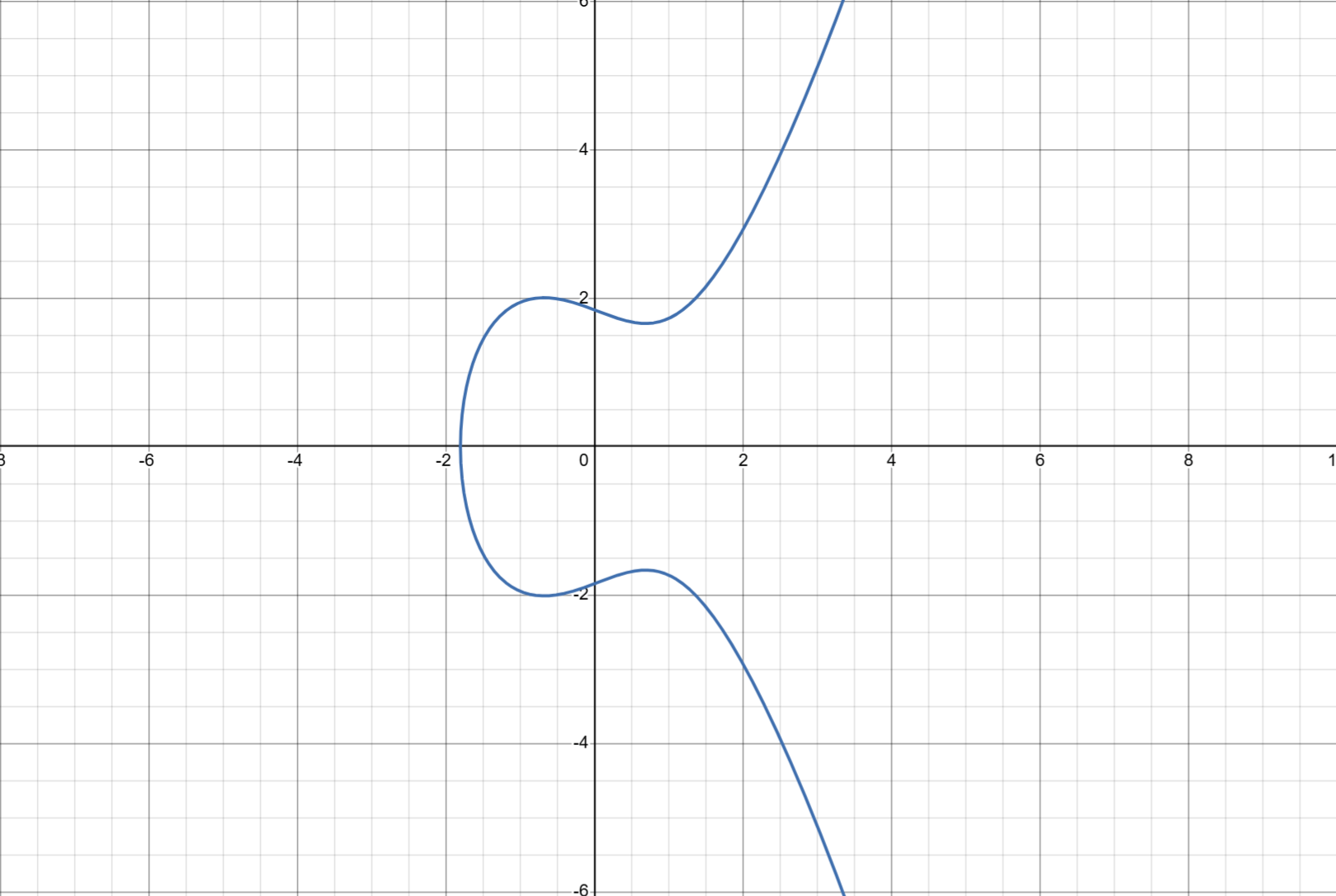
当这个方程表示的曲线是一条连续的曲线时,需要满足条件 4A3 + 27B2 ≠ 0 这时称为非奇异椭圆曲线，反之称为奇异椭圆曲线

奇异椭圆曲线都是形状有点尖或者有交叉

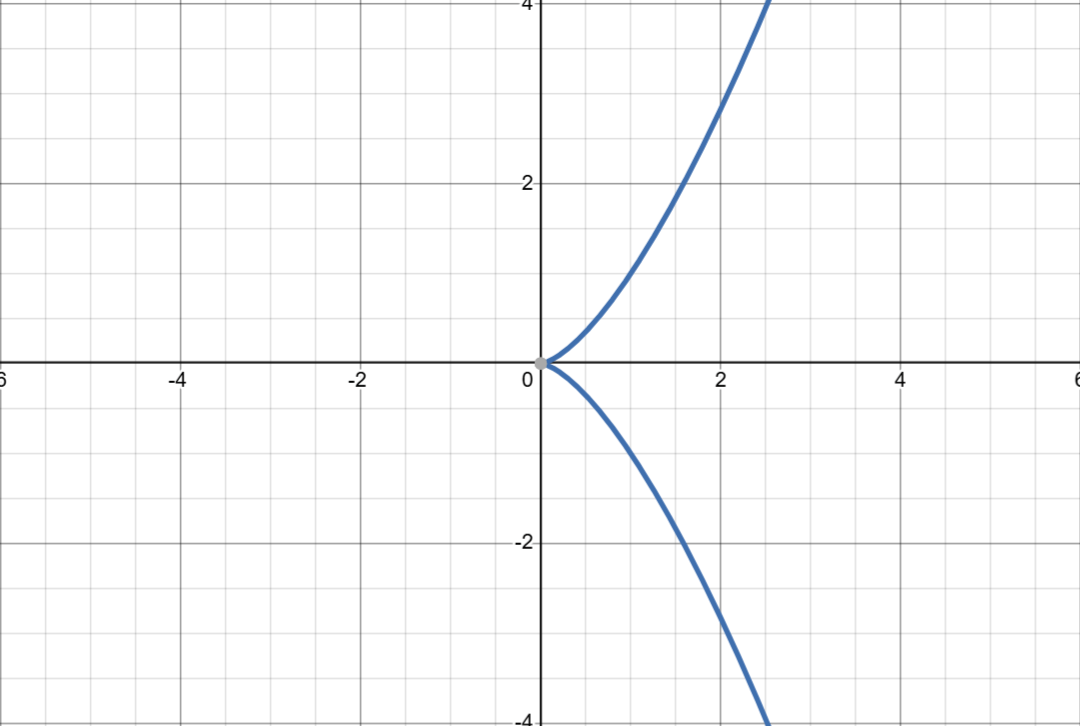
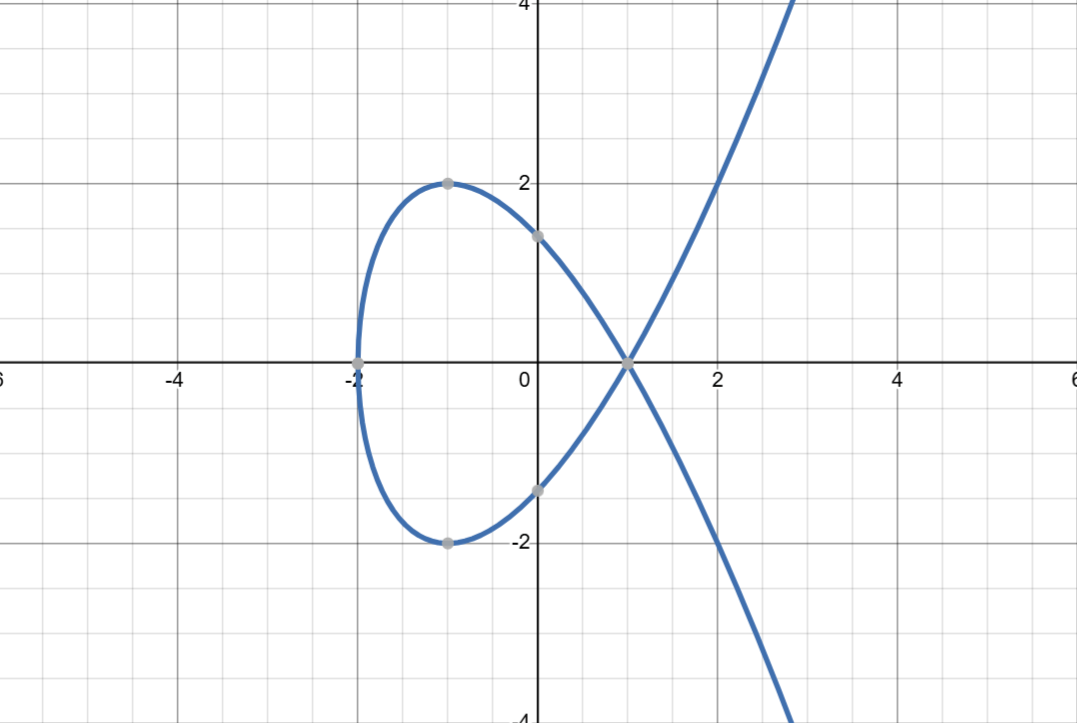
这些情况下的点加法会出现问题

下面来介绍一下点加法

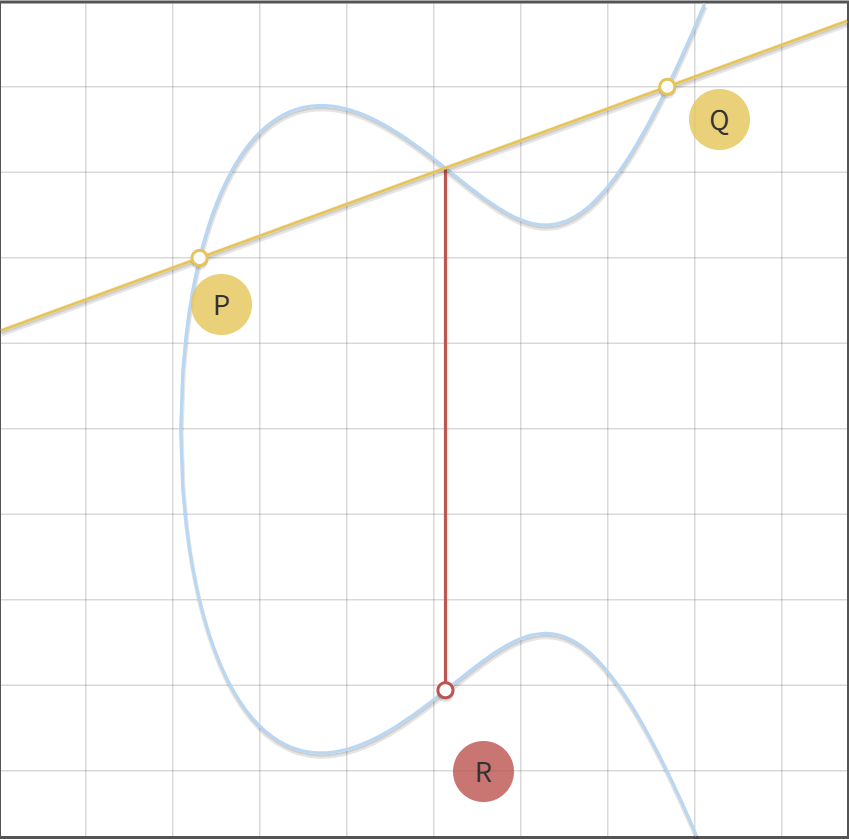
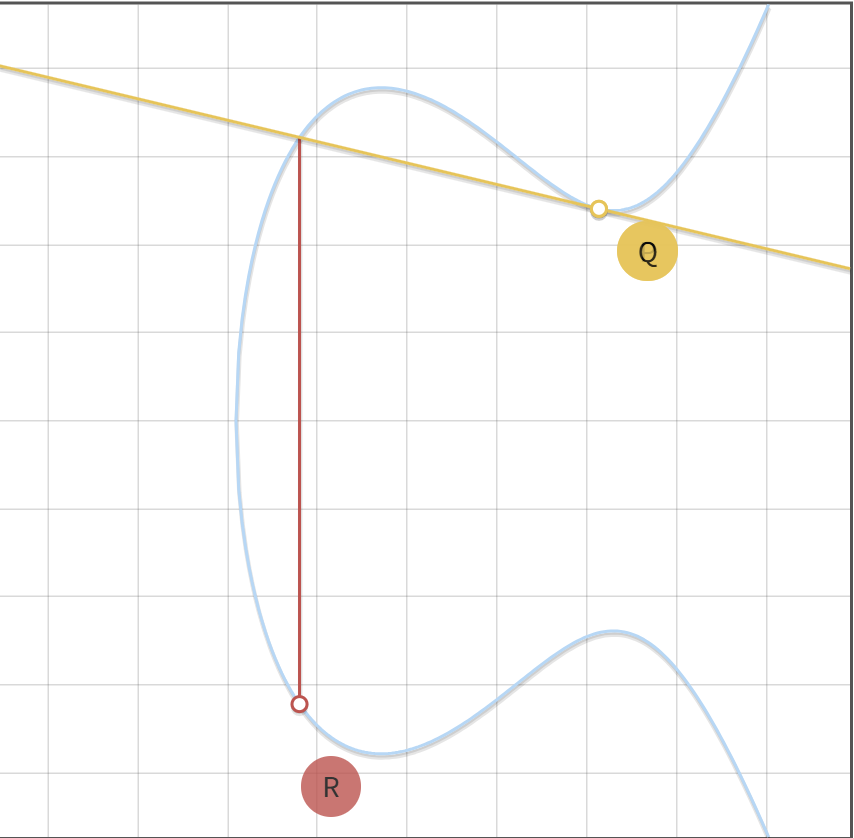
我们在椭圆曲线上定义加的运算，我在曲线上找到两点P，Q,现在想要计算出P ⊕ Q

首先我们连接P,Q两点，与椭圆曲线E相交于一点

相交的点关x的对称的点就是P ⊕ Q的点R

这里我考虑一个情况如果当P=Q的时候也就是P ⊕ P，该如何运算呢

其实还是一样的，只不过这次我们取过椭圆曲线E上的点P的切线，再与曲线相交后做关于x轴的对称点即可

现在还有种情况就是如果是无穷远点呢，也就是当P,Q关于x轴对称

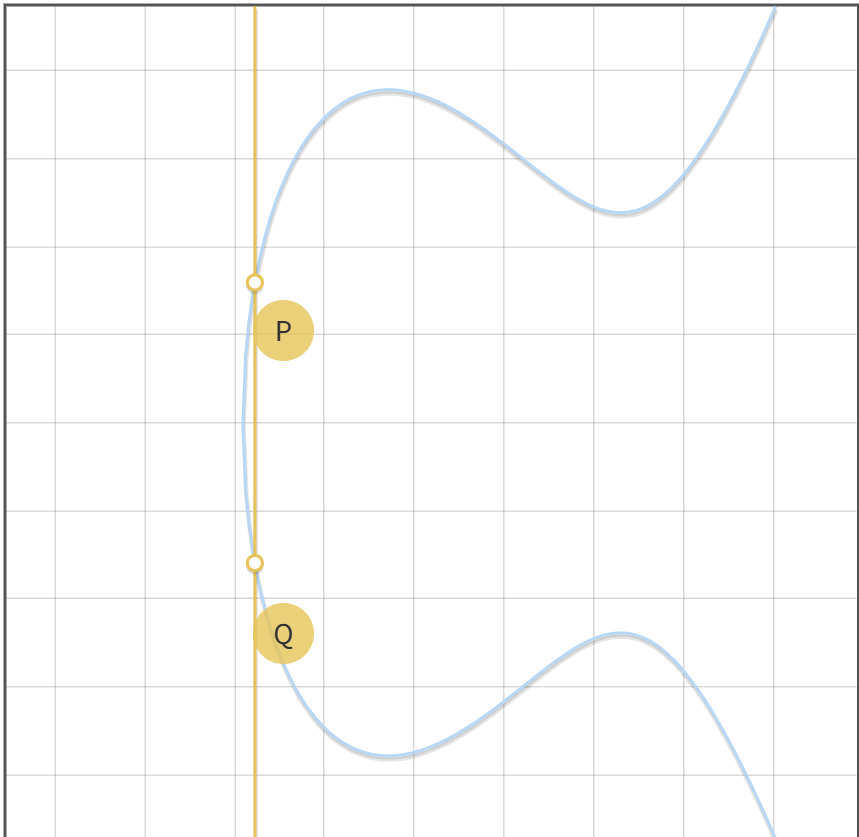
也就是P ⊕ P′ = 𝒪

这时候会发现 P ⊕ 𝒪 = P 𝒪也就是加法运算中的单位元

这个精妙的几何定义使得椭圆曲线上的点构成了一个阿贝尔群

也就是满足了封闭性，有单位元，有逆元，交换律的群

有限域上的椭圆曲线

安全领域说的椭圆曲线通常是说通过椭圆曲线定义出来的群，其范围定义在某个有限域，也就是所有的运算是在模p下进行的

sagemath 可以在有限域上建立椭圆曲线，并枚举所有点

1
E = EllipticCurve(GF(13), [3, 8]) E.points()

也可以进行其它的运算

1
2
E = EllipticCurve(GF(13), [3, 8]) 
print(E(1, 5) + E(1, 8)) *# (0 : 1 : 0), 无穷远点* print(E(12, 2) + E(9, 7)) *# (2 : 3 : 1)*

椭圆曲线离散对数问题

也就是给定了点P和nP,要推出n

1
2
3
4
E = EllipticCurve(GF(73), [8, 7]) 
P = E(32, 53) 
Q = E(39, 17) 
P.discrete_log(Q)

椭圆曲线加密算法的过程

公私钥生成:

1、首先构造一条椭圆曲线E，在曲线上选择一点G作为生成元，并求G的阶为n，要求n必须为质数

2、选择一个私钥d(k<n)，生成公钥P=dG

3、将公钥组E、P、G发出

加密过程：

这里选择一个随机整数k，计算出Q=kG,C=M+kP

解密过程： 使用私钥计算出M=C-dQ,得到明文M